This article accompanies Alan Couzens’ podcast with the Fast Talk Labs crew around applying neural networks to sports. In it, he dives into just what a neural network is and why it is a great solution to the daunting task of modeling real-world sports performance.
Like it or not, we live in the time of Big Data. Athlete wearables are ubiquitous and spit out megabyte after megabyte of ever advancing data. This data is increasing not only in magnitude, but also in the number of metrics being monitored: Power, pace, heart rate, normalized power/pace, decoupling, variability index, intensity factor, time in heart rate zone, time in power zone, time in pace zone, power-duration curve, heart-rate duration curve… TSS, TRIMPS, HRV, rMSSD, SDNN. You likely get the idea. This means that not only must the modern coach be aware of and able to explain these various metrics, they also need to be able to combine the information coming from these metrics in a meaningful way towards what ultimately matters— going faster on race day!
What is a neural network?
A neural network is a type of machine-learning algorithm that is modeled on the functioning of the brain. Back in 1943, two neuroscientists by the names of Warren McCulloch and Walter Pitts wrote a paper called “A Logical Calculus of the Ideas Imminent in Nervous Activity.” In it they expressed the functioning of neurons in the brain mathematically, fundamentally arriving at the “all or nothing principle” which expresses neuron activity in a very binary way – if the message from all of the input neurons is sufficient, a neuron fires. If it is insufficient, it does not. This binary on/off behavior didn’t take long to make its way to computer scientists who saw obvious connections to the same “on/off” behavior of bits in the machine.
Frank Rosenblatt ran with this “mathematical brain” concept and introduced the Artificial Neural Network, the “Perceptron” in his paper in 1958. This was a very simple mathematical model, adapted directly from the “all or nothing” concepts laid out by McCulloch and Pitts, where the weight of a group of model inputs was added up. If it reached a critical threshold, the “neuron” fired and a certain category was returned. If it didn’t reach this threshold it was not. We’ll give you an example of how this can be applied to your training later on, but first, you might be surprised to learn that this is not a red hot phenomenon.
AI from back in the day
Almost 50 years ago, a kinesiology professor by the name of Eric Banister took on the challenge of taking the available metrics (of the time) and relating them to the thing that really matters: performance. His paper, A Systems Model of the Effects of Training on Physical Performance, holds up well, even today. Banister took the approach of wrapping up training volume and intensity into one unit called a TRIMP (TRaining IMPulse). He then built a mathematical impulse-response model that related this TRIMP input to the athlete’s actual performance (on a rating scale against the current World Record so that different performance types could be assessed). This impulse-response model was later used (with Training Stress Score, TSS, in place of TRIMP) in TrainingPeaks Performance Management Chart (below).
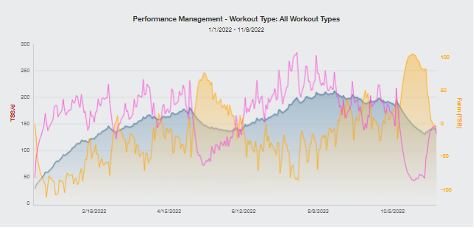
The blue line (CTL) represents a model of the athlete’s general “fitness” over the course of the season.
However, there is one key difference between Banister’s model and the ‘model’ used in the PMC: The parameters in Banister’s model were tweaked to predict actual performances rather than just showing a general ‘fitness’ trend. When the model was implemented in the PMC it lost this functionality and, in my opinion, lost a lot of its usefulness. These days, most coaches and athletes just roll with the default settings for the “CTL constant” (Tau1) and the “ATL constant” (Tau2) and no attempt is made to fit the curve to actual athlete performance. This is understandable, as manually fitting the curve to the individual athlete can be quite time consuming.
Additionally, the ‘impulse’ part of the original model was very simplified—wrapping up all that comprises a training session into a single number, initially TRIMPs and later, TSS. Anyone who has racked up 100 TSS via three hours of easy spinning versus a one-hour all-out TT will agree that they represent a very different stress on the system!
These shortfalls represent some pretty significant limitations when it comes to practically understanding the relationship between training and performance in a meaningful way.
So, ideally we want a training-performance model that:
- Models actual performance
- Is easily customizable to the individual
- Is able to take multiple different types of training as inputs
Putting it into practice
Let’s say that we want to build a neural network that predicts if an athlete is going to qualify for Kona.
We may not have a lot of experience in what features are important in determining if an athlete has a shot at qualifying so we decide to feed it three random features to start:
- Is their annual training volume greater than 800 hours?
- Is their average training intensity greater than 70% max heart rate?
- Do they own a dog? (bear with me!)
So, we have our features, we have some data. Now how do we train our neural network to determine what features are important and come up with a prediction?
In 1949, neuropsychologist Donald Hebb made the observation that “neurons that fire together wire together.” By feeding it instances of known data, the network “learns” what’s important by updating the weights of the input features that make a difference. A simplified example is shown below, highlighting how our network learns which of these features are important:
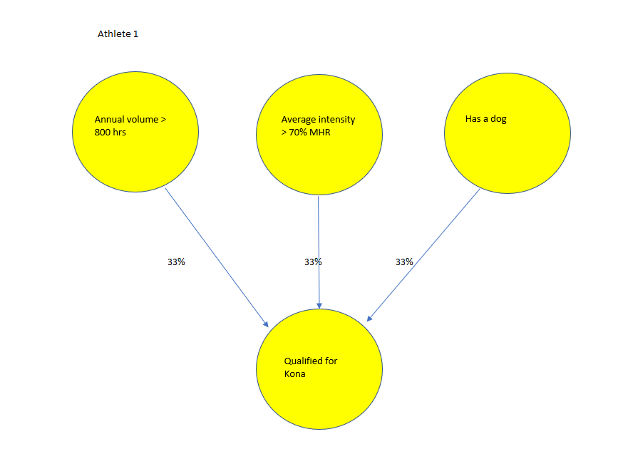
We start by training it with various examples of training data where we know both the inputs and the output, i.e., whether the athlete qualified for Kona.
Training example 1
In the first example we feed the network, all neurons are lit up (yellow). The athlete did train more than 800 hours, they did have an average training intensity of >70% max heart rate, they do have a dog and they did qualify for Kona.
All features have a 33% contribution to qualifying and, at this point, the network thinks each is equally important.
So let’s feed it another example…
Training Example 2
For the second athlete that we show the network, the 800 hours neuron is lit up, the greater than 70% MHR neuron is lit up, but the “has a dog” neuron isn’t lit up, as this athlete doesn’t have a dog, so the network dials down the weight of that connection to only half the weight (16%) since of the two observed instances it’s a 50/50 chance that having a dog is important, meaning this neural connection is less strong, less reliable. In other words, the “has a dog” and “Kona qualifier” neuron didn’t fire together this time so they became less “wired together.”
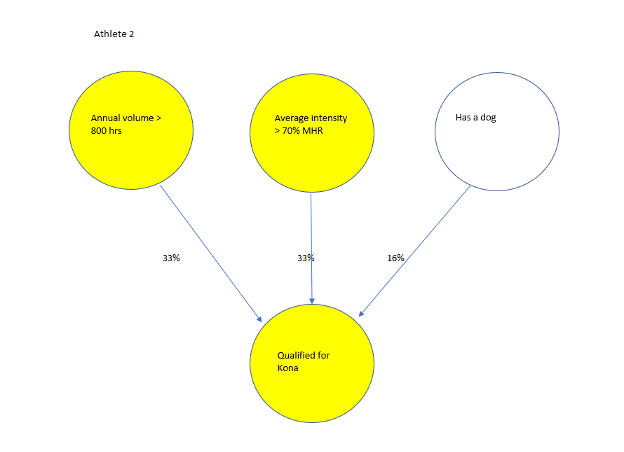
This whole practice is repeated for all available training data and the weights of the connections are progressively tweaked.
Over time, using this simple approach, the network figures out what features are important to the prediction and is then able to categorize the likelihood of a new prediction falling into that category.
For example, let’s say after iterating through all the training data, our final weights are as they appear above (the model learns that having a dog actually contributes positively to your chance to qualify!) and our threshold for the “Qualified for Kona” neuron to fire is 50%. We get a new athlete that trains 1,000 hours and has a dog but trains at a very low intensity (<70% max), so they get 0.33 + 0.16 = 0.48. Not enough to light up the “Qualify for Kona” neuron. Prediction: Will not qualify.
While this whole concept is very cool (and I do mean *very* cool), it doesn’t take too long to see that the above network has a big problem. Inputs and outputs have to be linearly separated, i.e., if I wanted to get a little more specific with high volume versus low volume and I instead wanted to look at actual hours of training, I’d need many training instances from each hour of training for this to work. Right now 799 hours of training gives you no chance of qualifying and the extra one hour tips you over the edge. So, we’d really want a whole lot of bins: 700-750, 750-800, etc., but then we’d need enough training data for each one of those specific bins.
Another problem is that we’d really like something with different levels capable of handling different interactions between the variables, e.g., if I had a node for 600 hours training volume and another for 800 along with an intensity of 70% heart rate and another for 80%, I’d like to be able to look at the combinations—maybe 600 hours plus 80% heart rate does the job, whereas just 600 hours or just 80% alone doesn’t. So, I’d need another layer, where there’s another node that the 600 hrs and the 80% MHR feed into. This structure is called a Multilayer Perceptron or, when many layers are stacked, a Deep Neural Network. However, this new structure creates other problems. How much do I update the weights on each layer, i.e., how much of each specific neuron contributes to my qualify versus no-qualify? When layers are added, the relative impact of each neuron in each layer is very tough to figure out. As networks get big, these issues start to become prohibitive. This fact is why neural networks fell largely out of favor as a promising route for A.I. researchers in the 1970s and 1980s.
What we need instead is something that is not a binary step function, that is either “right or wrong,” but a bendy function that can say “this neuron is a bit more important than what I previously thought.”
Welcome to the world of backpropogation
In 1986, Rummelhart, Hinton and Williams published a groundbreaking paper that showed that if we use a non-linear differentiable function (instead of the right/wrong) step function, we can apply the ‘Chain Rule’ of Calculus to it to pass the error back through all nodes of the network and have each node automatically updated to just be a little less wrong. This process of feeding a training example and having the network pass the error back through each neuron in the network to update the weights can be repeated automatically over and over again to progressively “tune” the network to reality.
Combining these two developments, the ability to account for combinations of multiple variables coupled with the ability to train these deep networks leads to a really powerful algorithm, an algorithm that can bend to approximate any function. In our context, a model that can bend to approximate very different load-performance relationships.
Novice athlete
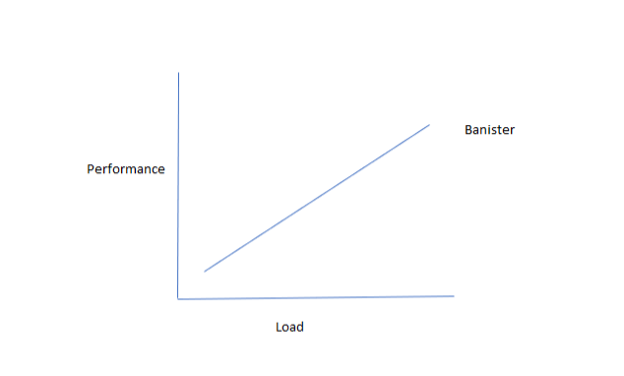
The Banister model is a linear model that says that more load always equals more performance. Experienced coaches know that this only holds true for novices just starting out. Once we get to a certain level, diminishing returns kick in and the model will start to deviate from reality.
Typical athlete (diminishing returns)
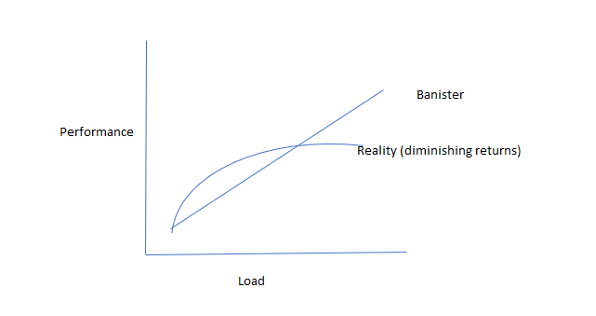
The typical pattern for most athletes over the course of a training season is shown above. Initially the fitness gains are strong, and then as load builds, the athlete gets less performance benefit from each additional unit of load. This is expressed as the well-known principle of “diminishing returns.” The Banister model cannot account for this phenomenon (unless we change the model constants frequently). A neural network, on the other hand, a model that can bend, is the perfect match for this pattern. Maybe even more important, the coach can sometimes see another pattern..
Overtrained athlete (inverted U)
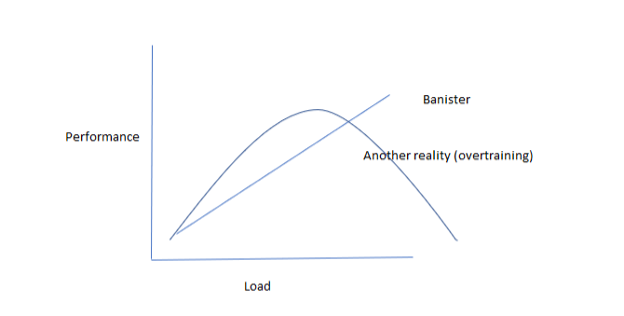
This might be the most important pattern of all that we want our model to be able to identify. Again, the Banister model with its “more load is always good” stance misses out on identifying this crucial deviation from that. A neural network, on the other hand, can bend and so it can approximate, and identify, this very important pattern.
Thinking Fourth-Dimensionally
But, we’re still not thinking fourth dimensionally…We’re still wrapping up volume and intensity into one number (load) when we express it as a plot like this. Neural Networks can do even better. Rather than just identifying critical load points where performance starts to fall off, a neural network can pinpoint specific volumes, specific intensities, specific volumes in different zones and, even more impressively and powerfully, the combinations between these variables, e.g., performance may start to fall with 300 hours at 80% but not 300 hours at 70%. This ability helps us to determine what specific volume/intensity combination is likely to be optimal for a specific athlete.
An example of this approach can be found in the paper “Modeling and prediction of competitive performance in swimming upon neural networks” by Edelman-Nusser et al.
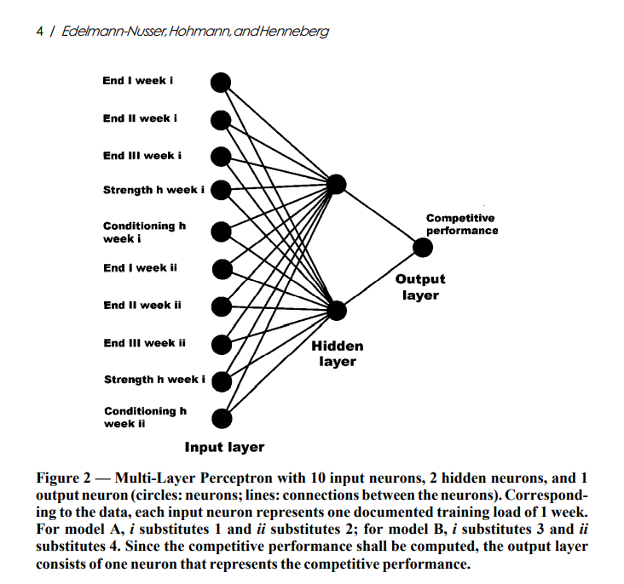
You can see a similar pattern to our simple “Will I qualify?” network, only this Neural Network has a lot more neurons, with inputs related to both time (week 1 v week 2) and related to the category of the intensity of the training (End 1 = <3mmol/L, End 2 = 3-6mmol/L, End 3 = 6-20mmol/L), along with neurons devoted specifically to additional strength and additional conditioning work.
The advantage to taking this approach over a simple TSS model is obvious—rather than just looking at the relationship between an “all-wrapped-into-one” training load number, we can model the relationship between specific training types. This has a lot more practical utility for the coach. Rather than just saying: “I want you to accrue 500 TSS this week,” we can say: “The model is suggesting two hours of Zone 1, one hour of Zone 2, 45 minutes of Zone 4 and no Zone 3 or 5 will lead to the highest predicted performance.” That is, we’re taking the model outside the two dimensional view of load versus performance and we’re thinking 10-dimensionally!
It should come as no surprise that this methodology offers superior predictive accuracy. In the referenced study, this neural net predicted race performance with an accuracy of 5/100ths of a second.
Conclusion
In conclusion, coaches and athletes are being bombarded with more sources of data than ever before, often to the point of “analysis paralysis.” Fortunately, what we need to make sense of this multitude of variables in a meaningful way already exists, in the form of Neural Networks. In this article (and the accompanying podcast) I hoped to give the coach a gentle introduction to how neural networks do their magic, along with some examples of how we can apply that magic to real-life performance prediction and, more importantly, evidence-based decision making.